Why do people think that we "prove" things in science?
Why do people think that we "prove" things in science and think a good attack against an hypothesis is that it is "unprovable," even though every assertion made by science is unprovable, as it can always be overthrown by a future observation? And why do they only attack things in science as "unprovable" only when it's some scientific hypothesis they have a political opposition to, while ignoring the fact that everything else in science is also unproven and cannot be proven?
When I say that all scientific theories are unprovable, I'm referencing the ideas of famed philosopher of science Karl Popper, who is well known for discussing the idea that a scientific idea must be falsifiable. In other words, there has to be some way (in principle, if not in actual practice) that you could have an outcome which contradicts a scientific idea.
Any idea which can be constantly shifted around so that any sort of evidence would fit it is, by Popper's definition, not a scientific idea. (This is why the concept of God, for example, is not scientific. Those who believe in God use pretty much everything to support their claim and cannot come up with evidence -- at least short of dying and finding that nothing's happened, which unfortunately yields little in the way of empirical data in this world -- which could, even in theory, refute their claim.)
One consequence of Popper's work with falsifiability is the understanding that you never really prove a theory. What scientists do is instead come up with implications of the theory, make hypotheses based on those implications, and then try to prove that specific hypothesis true or false through either experiment or careful observation. If the experiment or observation matches the prediction of the hypothesis, the scientist has gained support for the hypothesis (and therefore the underlying theory), but has not proven it. It's always possible that there's another explanation for the result.
http://physics.about.com/b/2011/03/26/scienceproof.htm
_________________
"You have a responsibility to consider all sides of a problem and a responsibility to make a judgment and a responsibility to care for all involved." --Ian Danskin
This is the scientific method, not just "Popperian methodology." The scientific method entails making a number of observations and coming up with a hypothesis based on them, a hypothesis that makes certain predictions about what you will observe in the future (i.e. the hypothesis is supposed to help constrain, make more predictable, what you will see). The hypothesis is vulnerable to falsification based on whether future observations match the predictions made by it. If they do match, then the hypothesis is supported, but it's always the case that a future observation can trash or at least limit the applicability of the hypothesis.
Take Newton's laws of mechanics: They have been falsified. However, we need not take a naive view of falsification, as Newtonian mechanics do make very accurate predictions about what will happen when it comes to dealing with physics on a human-scale. Where Newtonian mechanics fail are on the particle scale (and here quantum mechanics takes up the science) and on a cosmological scale (where relativity takes up the science). Quantum mechanics and relativity help fill up the gaps left by Newtonian mechanics and they make very accurate predictions that have been supported by multiple observations.
Making specific predictions and allowing for hypotheses to be vulnerable to falsification is how we make progress in science. If you make a hypothesis that does not permit falsification (i.e. you can always change the goal posts to prevent falsification), then the hypothesis isn't just not science, it's also useless, because it fails to make specific predictions about what we will see, and it fails to constrain and make more predictable what we expect to see, and that is because it is designed to not be vulnerable to any sort of contrary observation: The goal posts can always be moved.
That Newtonian mechanics made specific predictions and were falsifiable allowed us to make progress when we found situations where it failed to make the correct predictions. When that happened, we knew that what we had was not sufficient and were forced to go back to the drawing board in situations where the predictions failed to come up with new and better explanations that made predictions that were correct.
Were it not for the falsifiability of Newtonian mechanics, if the goal posts could always be moved around, then we would not have either quantum mechanics or relativity right now, because Newtonian mechanics would have become akin to a religious belief and there would have been no motivation to come up with something better.
_________________
"You have a responsibility to consider all sides of a problem and a responsibility to make a judgment and a responsibility to care for all involved." --Ian Danskin
When I say that all scientific theories are unprovable, I'm referencing the ideas of famed philosopher of science Karl Popper, who is well known for discussing the idea that a scientific idea must be falsifiable. In other words, there has to be some way (in principle, if not in actual practice) that you could have an outcome which contradicts a scientific idea.
Any idea which can be constantly shifted around so that any sort of evidence would fit it is, by Popper's definition, not a scientific idea. (This is why the concept of God, for example, is not scientific. Those who believe in God use pretty much everything to support their claim and cannot come up with evidence -- at least short of dying and finding that nothing's happened, which unfortunately yields little in the way of empirical data in this world -- which could, even in theory, refute their claim.)
One consequence of Popper's work with falsifiability is the understanding that you never really prove a theory. What scientists do is instead come up with implications of the theory, make hypotheses based on those implications, and then try to prove that specific hypothesis true or false through either experiment or careful observation. If the experiment or observation matches the prediction of the hypothesis, the scientist has gained support for the hypothesis (and therefore the underlying theory), but has not proven it. It's always possible that there's another explanation for the result.
http://physics.about.com/b/2011/03/26/scienceproof.htm
While no theory can ever be proved, the actual issue, according to Popper, whether it can in principle be disproved. That's what falsifiable means. In order to be considered scientific, there has to be a possible experiment or observation that can rule it out or prove it wrong, not something that can prove it right, which can never be done because of the problem of induction.
Crazy talk.
Heliocentrism was once a theory.
Yes, and it hasn't been proven either, at least not in the way that a math theorem can be proven. Rather, we gathered enough evidence to show that it's at least the most probable explanation. What happens in science is that the longer a theory resists falsification, the more we mount up evidence to support the theory.
Also, scientifically speaking, heliocentrism is still called a theory.
You don't understand what the word "theory" means in science. It's not the same way we use it in everyday speech where we think of "theory" as just a conjecture. A scientific theory is a well-substantiated explanation that's been confirmed repeatedly though observation and experimentation. So by that definition, heliocentrism is still a scientific theory as well as a scientific fact.
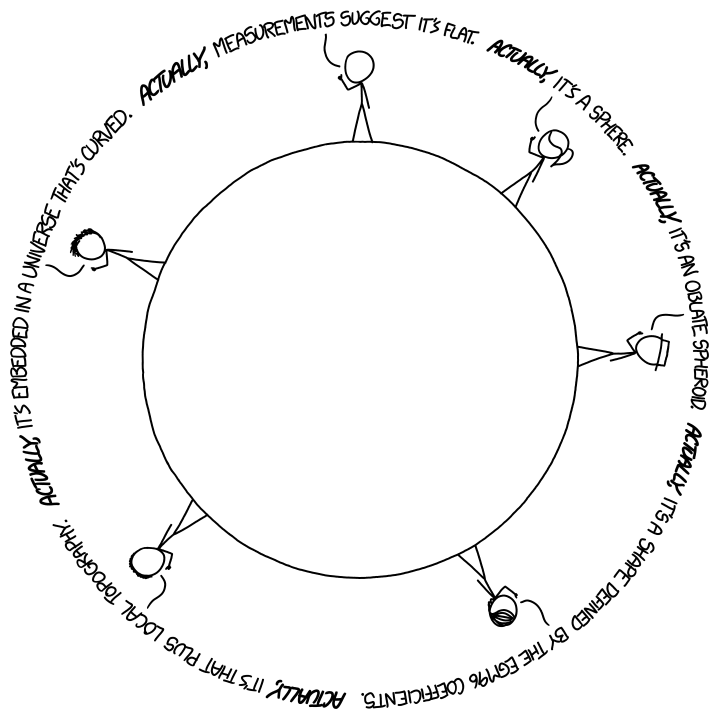
Think of it like this, Humanaut, the earth as flat vs. earth as a sphere. Which one is correct? Neither! The earth is in fact an ellipsoid that very closely approximates a sphere, but is not a sphere.
Nevertheless, to say that saying that the earth is a sphere is just as wrong as saying that the earth is flat is, as it has been said, wronger than wrong.
Assuming the earth is a sphere works in many applications and simplifies calculations, even though the earth we now know is not truly a sphere. On the other hand, assuming the earth is flat really only works if you're making maps or surveying for small areas on earth, and works in far fewer applications than assuming that the earth is a sphere.
_________________
"You have a responsibility to consider all sides of a problem and a responsibility to make a judgment and a responsibility to care for all involved." --Ian Danskin
Crazy talk.
Heliocentrism was once a theory.
Actually, the definition of a theory is, a coherent system of ideas. EVERY system of ideas is a theory, only a theory, and nothing BUT a theory. Let me expound upon this by providing something very close to the formal definition of a theory. A theory is a system consisting of a small ('small' isn't defined) finite number of axioms (statements both mutually- and self-consistent, about the system we are attempting to describe with our theory). Theoreticians who work within a given theory will then apply valid logical reasoning to deduce theorems from the axioms and other already-proven theorems. A concluding statement of this reasoning process is called a 'theorem'. The reasoning process itself is called a 'proof', because provided the theoretician used only valid deductive reasoning, the conclusion is guaranteed to be true if the axioms are true. The words 'theory' and 'theorem' are Greek, where 'theory' is simply the plural form of the word 'theorem'. So, formally, a theory is the collection of axioms and provable theorems.
So, a theory is always and will always be precisely (no more and no less than) a system of ideas that attempt to capture, model or explain another system.
Hence, most things are theories. Certainly all theories of science (relativity, heliocentrism, geocentrism, genetic theory, the germ theory of diseases, etc...). But also various systems of ideas that describe all the religious concepts (the theory of the soul, for example). Philosophy constructs things that often don't initially seem like theories, such as various theories of ethics which try to rationalize the 'right' from the 'wrong' (Utilitarianism, relativism, etc.); and theories of aesthetics, theories of the state, theories of justice, etc.
Now there is just one more thing about a theory: any non-trivial theory has an infinite number of theorems.
If a theory has an infinite number of theorems it's impossible to find and construct proofs for all theorems in the theory. In science it is possible to construct a proof of a statement, but science does have the additional requirement of clinical evidence. Now, given that a theory consists of an infinite number of statements, it's impossible to prove them all in a finite amount of time. Hence it's impossible to prove a theory. Theories are the results of the human mind attempting to describe a system. But given that one CANNOT prove all statements in a theory, one CANNOT prove the theory is true. On the other hand, as noted by Karl Popper, disproving just one theorem in a theory DOES invalidate the entire theory. The theory needs to be revised. After revision we have a new theory. The new theory may be quite similar but it's NOT the same theory. Just as two dimes minted in different years are not identical given that they differ by just the year stamped on them.
Heliocentrism is as much a theory as a stone is a theory. It is directly observable; a self-evident metaphysical existent; an axiom in itself. There is no problem with induction as such. It is perfectly possible to directly describe certain aspects of nature as it is, but to explain why it is as it is, is not always as straightforward.
Something cannot be both a theory and an axiom, which is what you claim in your first two sentences above. Theories are constructed out of axioms using deductive reasoning (just as a wall might be constructed out of bricks. Bricks aren't walls, they are components of walls. Compositional reasoning such as this are common fallacies.). While induction has its uses, no finding of induction can be called a theorem. Induction deals with probability rather than the certainty of deduction. Hence, the findings of induction cannot themselves be certain. Hence, neither sound nor valid conclusions follow from inductive reasoning. The strongest label we can apply to the finding of an induction is 'cogent' -- which is no where near as strong as the label 'sound' (which can only be applied to the conclusion of some deductive arguments). Hence, inductive findings cannot be used to base new arguments upon for purpose of expanding the theory. So, 'heliocentrism' is not both a theory and an axiom.
Moreover, 'heliocentrism' is a conclusion... a finding... Something that follows from simpler notions. For example, Heliocentrism can be shown to follow from Newton's Laws of Motion. In fact this is the primary drive of Newton's Principia. First he shows that things on earth like cannon balls follow his laws. Then he uses the same exact laws to describe how the moon circles the earth. Finally he uses his laws to derive Kepler's Laws of Planetary motion (heliocentrism). Thereby, Newton, in his one book proves that all motions on earth and in heaven are governed by the same laws.
A 'stone' cannot be a theory. The string of symbols 'stone' contains no axioms. An axiom is necessarily a proposition (statement that makes a claim). One can only reason from statements that make claims. Let me provide a very simple example. The following is a valid deductive argument with two premises (I place one proposition per line so that the formal structure will be clear).
a. If it is raining, then the ground is wet.
b. It is raining.
------------------------------------------------------
c. Therefore, the ground is wet.
If statements a and b were axioms of a theory, then c would be a theorem. If 'stone' were a theory, or an axiom, or even a proposition, you would be able to construct proofs (such as those above) with it. Since you cannot, 'stone' is none of those things.
In Aristotelean logic, the string 'stone' is called a term, something combined with other things to form a proposition.
In Frege-Russellean logic (classical formal logic of Frege and perfected by Bertrand Russell), 'stone' is called an object, a component of any classical logic that uses the notion of predicates.
Formal linguistics (formal meaning without regard to meaning) which includes formal logic, formal reasoning, and all the derivative systems or formal symbol manipulation are my special interest, and has been my special interest since I was in grammar school where I used to invent such systems on my own... long before I ever studied any such system. I have studied these systems extensively, originally I was interested in artificial intelligence, natural language processing and machine translation. After several years of living in text books on these subjects I began to further specialize my interest in logic. I studied the systems of classical logics quite literally to exhaustion (not my exhaustion, but until I exhausted of the subject itself). After that I got into proving theorems about logic itself (a discipline called meta-logic, or meta-theory). Today I am far deeper studying the philosophical implications of formal logical systems in particular and information theory in general.
I am less well versed in systems of non-classical and deviant logics. For the most part they tend to be pretty gimmicky - doing little or nothing more than can be done with classical logic -- though there are exceptions. I follow Susan Haack's convention of classifying systems which merely build upon Russell's logic (such as modal logics), as a subcategory of classical logics called extension logics. This is the most reasonable system given that extension logics remain within the classical logic paradigm, while non-classical and deviant logics DO stray from the classical logic paradigm.
| Similar Topics | |
|---|---|
| ali g on science |
30 Dec 2024, 1:38 am |
| new things |
04 Nov 2024, 9:28 pm |
| Washing Things |
07 Nov 2024, 10:25 pm |
| How do I take things less personally? |
04 Jan 2025, 9:34 pm |