LoveNotHate wrote:
naturalplastic wrote:
LoveNotHate wrote:
I like irrational numbers, like "square root of 2", because they make you think.
How can a number that never terminates, possibly exist in reality?
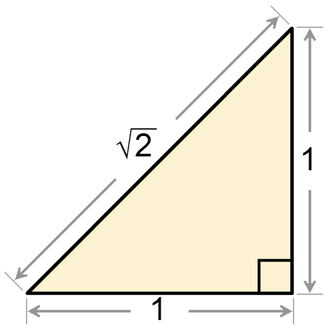
The irony is that not only do irrational numbers exist, they are majority of numbers. Its the rational numbers (integers, and fractions that have a terminus, or a repeating pattern in their digital form) that are the exceptions.
Sure, they exist in your mind, like vampires and werewolfs.
However, how can a number that never terminates represent a definite length in reality?
Get real.
ALL numbers "only exist in your mind like vampires".
What do you think most lengths are?
If you take a yardstick and just randomly hit it with an axe the axe will not likely cut the yardstick right at designated marking for a number of inches, nor right at a half inch, or a quarter inch, etc.
Most points on a yardstick are between the man made markings for the man made units of measurement on the yardstick. And they are not located at evenly divisible fractions of those manmade markings either (use your imagination and imaging you zeroing in on the yardstick down to the atomic level and beyond). Most atoms on a yardstick are at positions on the yardstick that can only be described as being at irrational number decimal units of the inches, or centimeters used on the ruler.

